读《哥德尔、艾舍尔、巴赫》后的感想

intro

在此 quote 一条十多年前的豆瓣热评，虽然仅用这句话来评价这本书还是过于神话它了，但是也足可本书的震撼：

世界上只有两种人：一种是读过此书的人，一种是没读过的人。

而在我看来，之所以这本书让读者认为它如此特殊，主要有两点：

其形式极其优美和有趣，侯世达在本书本身的文章写作上刻意模仿了很多赋格和卡农的手法，形成了一种逻辑诗歌般的风格（或者你可以说是文字游戏）。
这是一本跨越领域众多，但是又形成了惊人和谐的书。从哥德尔对形式系统的绞杀出发，竟能与巴赫规整的乐曲、埃舍尔幽微的画作形成悠扬的和弦，这种统一性怎能不让人觉得似乎抓住了一丝世界的真相呢？

特在此以主题为单位简略回顾本书。但是因为这本书有非常多内容其实是零碎的，我在这里其实会漏掉太多东西。

形式系统与哥德尔不完备定理

哥德尔不完备定理第一定理：任何自洽的形式系统只要蕴含了皮亚诺算术公理，就可以在体系中构造不能被证明的真命题，从而得出不能体系不能导出所有真命题，也即体系是不完备的。

哥德尔不完备定理第二定理：任何自洽的形式系统只要蕴含了皮亚诺算术公理，就不能证明本身的自洽性。

形式系统指的就是用特定的规则和符号组成的系统，比如本书中最重要的 TNT 系统，形如 $\forall a:(0+a)=a$ 。

对一个形式系统来说，其本身是没有任何的意义的，也就是说形式和意义应该是完全分离的。如果说我们可以赋予一个形式系统以意义，那只是因为这个形式系统的表现我们想要赋予的意义之间存在着一种同构。

这里最典型的例子可能就是欧几里得几何，理想来说欧几里得所描述的「点」、「线」应该是一种纯粹的形式符号，应当与现实中的「点」、「线」区分开来。而之所以欧几里得几何可以用来描绘现实，是因为这套形式系统中的「点」和「线」与现实中的存在一定意义上的同构。因此，几何的形式系统应该要是可以独立于现实来推导的，勇于做出这样的看起来有悖于现实推导的结论就是去掉第五公设，得出罗式几何和黎曼几何。

还有一个更简单的例子是这样的一个形式系统 $- - -q - p - -$，我们完全可以说其意义是「三等于一加二」，也完全可以说是「三减一等于二」，也还可以是更多的只要你能想到同时觉得是存在同构的意义。

而这里的皮亚诺算术公理是皮亚诺试图使用几条公理来将我们一直在使用的自然数形式化。与欧几里得类似得，他提出了五条公设。为了和现实中我们已经熟知的意义区分开来，我们可以使用一些其他的词来指代形式系统中的概念，因此皮亚诺公设大概是长这样的：

怪物是一个神怪
每个神怪都有一个元，元也是神怪
怪物不是任何神怪的元
不同的神怪有不同的元
如果命题对怪物为真，且假定它对一个神怪为真时，对神怪的元也为真，则命题对所有神怪都为真

所以在哥德尔定理里面提到的「只存蕴含了皮亚诺算术定理」的意思就是，只要这个形式系统有我们描绘自然数的形式系统那么强大。因此哥德尔的这两条定理也就可以说是：

第一定理：数论体系中可以构造不能被证明的真命题，从而得出不能体系不能导出所有真命题，也即数论体系是不完备的。
第二定理：数论体系不能证明本身的自洽性。

也就是说对于第一定理，哥德尔只需证明，有这样一句话 $G$，它在形式系统中，但是你无法证明它是不是定理（也就是是不是能被证明的真命题）。而实际上， $G$ 应该是要在说：「$G$ 不是一个 TNT 定理」，其实也就是说谎者悖论的形式系统版本。

但是问题就是，这样的一个 $G$ 是如何可能被构造出来的呢？我们可以看到，这句话的核心运用了一种「自指」的方法，所以我们要做的关键就是完成这种自指的构造。在说谎者悖论等非形式系统的自指中，「我说的这句话是假的」中的「我说的这句话」形成了自指，但是我们实际上这句话要完成自指的功能是需要很多的外部信息的。也就是说，我们之所以知道「我说的这句话」这几个字指的就是这句话，是因为更多的 context 提供给了我们以这样的背景知识，而我们要做的自指，应该是一种绝对的自指。

为了达成这样的自指，我们需要使用一个技巧叫做「哥德尔配数」，其实也就是将我们形式系统中的符号全部 encode 成数，然后将其印符规则使用算数规则来描述。通过这样的一层额外的配数，我们就可以在形式系统中去谈论这个形式系统本身的定理。

对于这个 $G$，我们还可以看到一种更加一般的模式，也就是「一个公式中代入了它本身」，我们可以将这种模式写成一个单独的方法，叫做 Quine。由于我们要代入的实际上是它本身的哥德尔配数（也就是算术化之后的结果），因此可以将其写作 $ARITHMOQUINE\{a’, a’’\}$，其中 $a’’$ 就是将 $a’$ 的哥德尔配数代入它本身的结果。

同时我们还需要定义一个符号 $TNT-PROOF-PAIR\{a, a’\}$，来表示在 TNT 形式系统中通过 $a$ 这样的过程，可以得到 $a’$ 这样的定理。其实也就是说 $a’$ 是 TNT 的定理，同时又给显式得给出了其推导过程。

于是我们就可以写出这样的一个串： \[\sim \exists a: \exists a’:<TNT-PROOF-PAIR \{a,a’\} \land ARITHMOQUINE\{a’’, a’\}>\] 其意义是：不存在有 $a$ 和 $a’$，使得 $a’$ 是 TNT 的一个串（是证明对的结果），然后同时也是 Quine 的结果。也就是说形式系统中没有一个串是 Quine 的结果。作者把这个串取名叫做 $G$ 服。

然后是最后一步：将 $G$ 服进行算术 Quine，就得到了 $G$： \[\sim \exists a: \exists a’:<TNT-PROOF-PAIR \{a,a’\} \land ARITHMOQUINE\{SSSSSSSS…0, a’\}>\] 其意义是：不存在有 $a$ 和 $a’$，使得 $a’$ 是 TNT 的一个串（是证明对的结果），然后同时也是 $G$ 服 Quine 的结果。也就是说

$G$ 服 Quine 的结果不是形式系统的串。
而我们知道，$G$ 服 Quine 的结果正是这一条串 $G$。

所以 $G$ 就是我们要找的那一条说「我不是定理」的串。这里技巧的核心其实正是 Quine，形成自指的矛盾的正是这个串中的 Quine：因为我们既在句子中描述了 Quine，对句子进行了 Quine。

至此，哥德尔定理就得证了，这条 $G$ 的存在就是形式系统无法完备的万恶之源。

于是：

两千多年以来那么多数学家的梦想就此破灭了，我们现在可以知道：「可证性」是永远弱于「真理性」的，没有一个形式系统可以证明出所有的真理。20 世纪初希尔伯特形式化数学的宏伟计划也就此泡汤。
人的认知——同样作为一个（足够强大的）形式系统——也是有界限的。我们的头脑中无法同时容纳一句话既是真的，又是假的这样的两件事情。
跳出系统是无法做到的（系统内的方法无法证明系统本身，哥德尔第二定理）。

数理逻辑与分子生物学同构的形式系统

候世达认为生物学上遗传的工作方式与我们前面描述的 TNT 形式系统有着高度的相似性。

我们知道遗传物质工作的大致流程：mRNA 去复制 DNA （转录），然后传输到细胞质的核糖体上，核糖体使用周围盘旋着的 tRNA （附着氨基酸）来根据 mRNA 的信息生成蛋白质（翻译）。在这里 tRNA 就像是一种映射，让核糖体可以根据从密码子得到氨基酸。而 DNA 在此仅指示蛋白质的一层结构，但是当蛋白质被合成之后，它们自己就会折叠成复杂的形态，形成三级结构。

但是其实在这个转录和翻译的过程中，本身也需要它们的结果——蛋白质——形成的酶来参与，而酶的主要功能主要是由其这些形态也就是三级结构来决定的。同时，核糖体想要解出 DNA 包含的内在消息，就需要 tRNA 这个映射，而 tRNA 本身也同样是通过 DNA 来生成的。

我们在其中看到了一种纠缠关系，看起来好像因为存在这样的 recursion，所以整个系统没法工作，这与事实完全不同。而在这个系统中，我们可以看到它与 TNT 的对应关系（直接拍了书）：

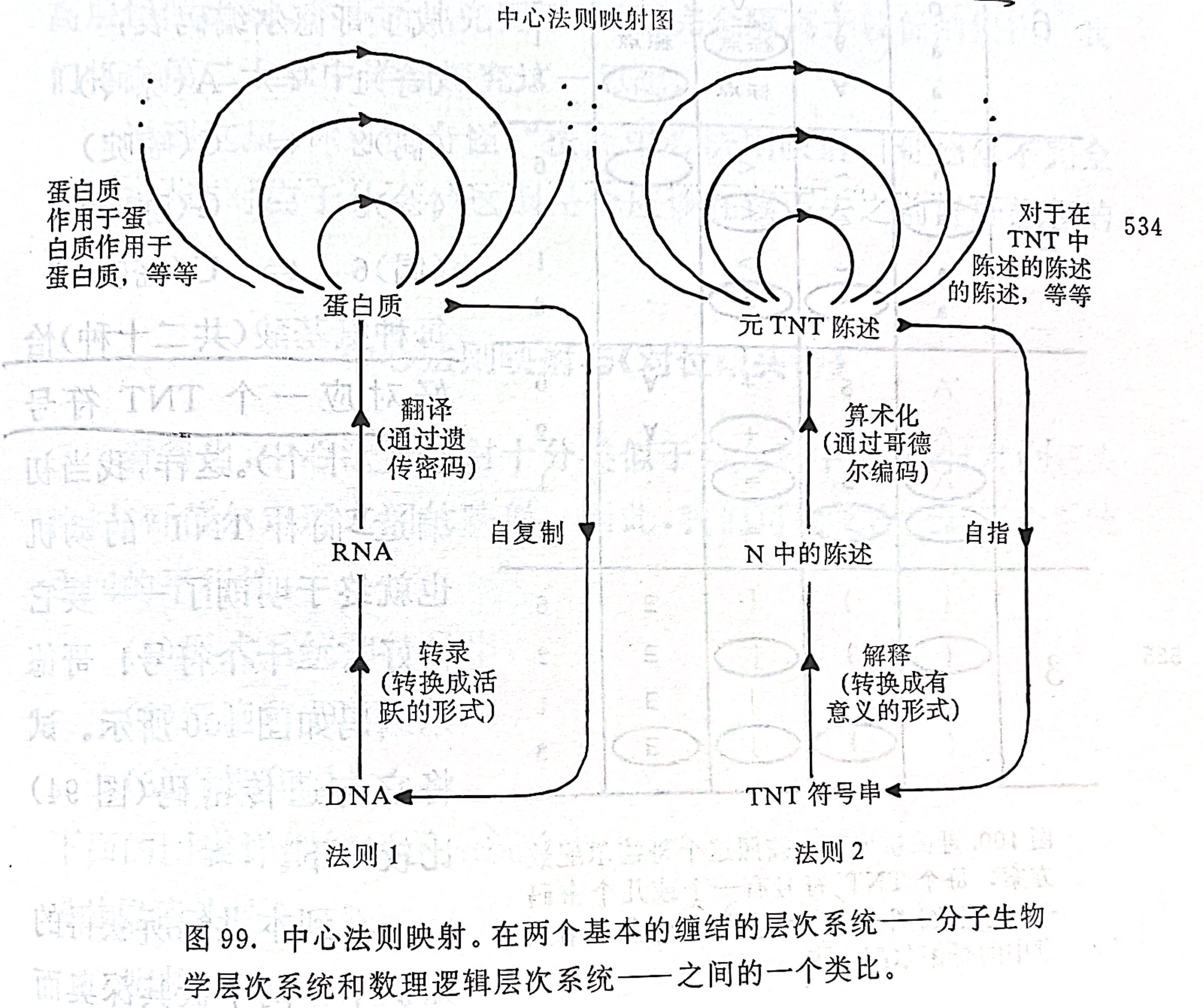
这里最引人注目的就是这个可以无限叠加的大圈，也就是说这个形式系统的运作在这一点上实际上是可以进入非常多不同的层次的。DNA 在这个大圈的某个（或者某几个）高层上可以自我复制，TNT 在这个大圈的某个层次上可以谈论自己。也许智能之所以能成为智能，生命之所以能成为生命，其中的核心秘密就在这个可以跨越无穷层次的规律。

埃舍尔与巴赫

本书谈论的一些核心概念如悖论、自指、递归、跳出层次都在埃舍尔的作品里有清晰的体现。

在这幅《相对性》中，确定一个形式系统的意义的过程实际上是用从外部引入的「外部意义」去固定内部的未定项的意义。楼梯的意义是比较明确的一种外部意义，而我们看的过程中需要用借用这种外部意义来理解剩下的部分的意义，但是与 qp 系统这样比较明确的形式系统相比，实际上楼梯之外的未定项无法得出一个「可理解」的系统。

这幅《龙》可以说完全就是哥德尔第二定理的视觉化表达：作为一条处于二维的龙，它一直试图从一个面穿出，但是不管它如何努力，仍都永远在这个二维的系统内。超越系统也许是永远也无法做到的事情。

其他其实还有很多，比如《画廊》非常像是在说 $G$ 是如何构造的，而《画手》则让人忘记了系统外的埃舍尔的那只手。

至于巴赫，他所常用的卡农这种技法实际上是用主题和不同声部的副本来构造整首曲子，这种副本虽然不是完全一样的拷贝，但是保留了非常多原始数据的信息，这种方式其实就是一种同构。而其赋格曲的杰作《音乐的奉献》则很像是一首 meta 赋格：用自指的方式在很多不同的层次上谈论自己。而他在 BWV 591 中急速变换曲子的主调音，让听众在其中迷失方向，以达到非常独特的体验。向我们证明了：我们脑海中所能维持的 stack 是极其有限的，一定程度上揭示了某种大脑对于音乐的处理方式。

另外，巴赫与埃舍尔还在《螃蟹卡农》这个作品上面形成了直接的同构。他们两个人的同名作品都使用了非常相似的技法：巴赫将主题与其回文形式叠加在一起，而埃舍尔直接将正向和反向的螃蟹密铺在了画上。

人的智能与人工智能

本书的一个核心讨论点就是：人类的智能是如何运作的？而真正的人工智能是否是可能的，是如何可能的？对于这两个问题，候世达其实并没有给出太清晰的答案，但是说了很多他的猜想。

我们大脑的结构可以看成是一个非常复杂的多层形式系统。这个形式系统的低层是神经元网络，神经元网络通过各种化学信号而在上层汇聚成真正的智能，在这些不同的层级中存在一件事情的非常多不同的同构。

那么大脑是不是形成一个智能所必要的呢？我们用电子元器件来模拟大脑的神经元网络，用更上层的软件来模拟大脑一层一层的符号，是不是就可以造出真正的和人类智能无差的人工智能呢？或者，如果我们真正了解了各层是如何工作的，我们是否可以将大脑的软件和硬件剥离开呢？也就是说是否可以将一个人的所有思想 port 到另一个同样底层是神经元网络的大脑中呢？所以如果人类智能是可 port 的，或者说是可抽取的，同时大脑的底层是可以用电子元器件来模拟的，那么人工智能就一定是可行的。

那么自由意志是如何形成的呢？人类智能的这一套形式系统，是如何做到跳出形式系统本身的设计规定，从而产生「自我」意识的呢？候世达在这里认为，自我同样是某个符号层的的一种概念，而当这个自我概念出现以后，外界的刺激就会被这个自我的概念所接管，而其内部是一堆由各种层次的符号纠缠的结构，这些刺激会被淹没在这样纠缠的结构中。此时程序就无法精准控制系统内的每个行为的细节，只能通过一种「直觉」的方式来控制整个系统的工作方式。而有了直觉时候，自我意识、各种意义也许就会在这个形式系统中出现，此时我们也许就可以认为它成为了一个真正的智能体。而在这之后，各种我们认为的真正智能体的特征，比如创造力和个人意愿等，都会在这样的交错的形式系统中迸发而出。